
Now that you have the two basic equations for the production of nutrient solutions, we want to use them to calculate the amounts of fertilizer required for a nutrient solution recipe.
If you are not familiar with the two equations, read this first: Hydroponic systems: Calculating the concentrations of nutrient solutions using the two equations.
Here is our problem: We want to use a modified Sonneveld solution (Matson and Peters, Insidegrower) for herbs in an NFT system. We use two 5-gallon containers and injectors set to a concentration of 100: 1 and call them storage tank A and storage tank B. How much of each fertilizer do we have to put in each storage tank ?
You may be asking: why two storage tanks? This is due to the fact that certain chemicals in our fertilizer solution react with each other as soon as they come into contact with each other. In all nutrient solutions ( fertilizer mixtures ) you have calcium, phosphates and sulfates - among other things, these three chemicals for all plants vital are. The last two react with calcium and are no longer present in the form we need in our nutrient solution. They connect to each other and fall to the bottom of the container as white flakes ( precipitates ). Therefore, phosphates and sulfates must be kept separate from calcium and, when introduced into the nutrient solution of the ( system, saved from direct mixing by means of a dosing pump or measuring cup ).
Modified Sonneveld recipe for herbs
| element | concentration |
| nitrogen | 150 ppm |
| phosphorus | 31 ppm |
| potassium | 210 ppm |
| calcium | 90 ppm |
| magnesium | 24 ppm |
| iron | 1 ppm |
| manganese | 0.25 ppm |
| zinc | 0.13 ppm |
| copper | 0.023 ppm |
| Molybdenum | 0.024 ppm |
| boron | 0.16 ppm |
These are the fertilizers that we will use. Some fertilizers contain more than one nutrient in the recipe, while others contain only one. Here is a small overview Commercial fertilizer from which you can put together your recipe
| Fertilizer |
Contained nutrients
(Nitrogen phosphate potassium and other nutrients)
|
|---|---|
| Calcium nitrate | 15.5-0-0, 19% Ca (calcium) |
| Ammonium nitrate | 34-0-0 |
| Potassium nitrate | 13-0-44 |
| Potassium phosphate monobasic | 0-52-34 |
| Magnesium sulfate | 9.1% mg (magnesium) |
| Sequestrene 330 TM | 10% Fe (iron) |
| Manganese sulfate | 31% Mn (Mangan) |
| Zinc sulfate | 35.5% Zn (zinc) |
| Copper sulfate | 25% Cu (copper) |
| Boron | 11% B (Boron) |
| Sodium molybdenum | 39% Mo (molybdenum) |
The first thing you notice is that we have three sources of nitrogen (calcium nitrate, ammonium nitrate and potassium nitrate), have two sources of potassium (potassium nitrate and potassium phosphate monobasic) and one source of calcium (calcium nitrate) and phosphorus (single-base potassium phosphate). We can start calculating the calcium or phosphorus in the recipe because only one fertilizer provides each nutrient. Let's start with calcium.
The recipe provides 90 ppm calcium. We calculate how much calcium nitrate we need to use to achieve this by using the first of our two equations.
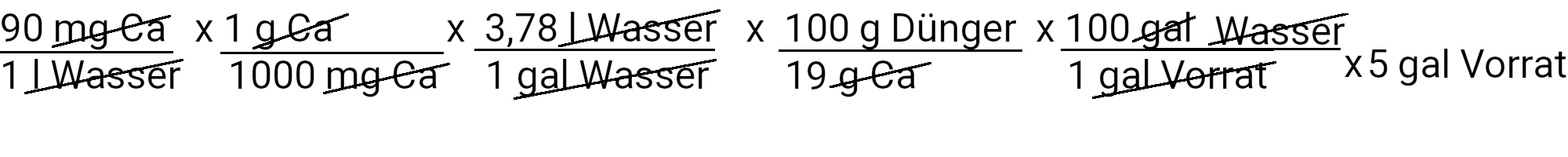
We need to add 895.3 g calcium nitrate to get 90 ppm calcium. However, calcium nitrate also contains nitrogen. We use the second equation to determine how much nitrogen should be added in ppm.
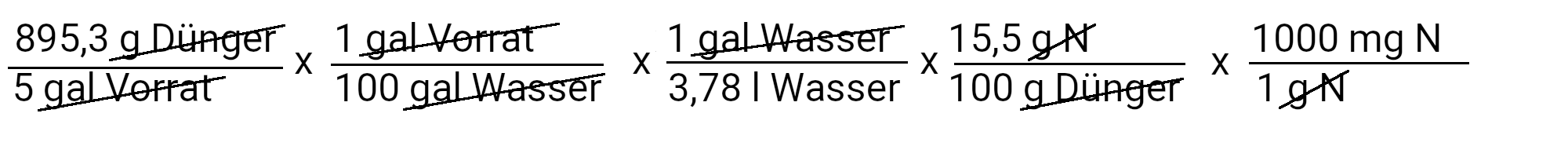
We add 73.4 mg N / l or 73.4 ppm nitrogen. Our recipe provides 150 ppm nitrogen. If we subtract 73.4 ppm nitrogen from it, we have to add 76.6 ppm nitrogen.
Let us now calculate how much single-base potassium phosphate we have to use to deliver 31 ppm phosphorus.

We need to add 262 g of potassium phosphate monobed to get 31 ppm phosphorus. However, potassium phosphate also contains single-base potassium. We use the second equation to determine how much potassium should be added in ppm.
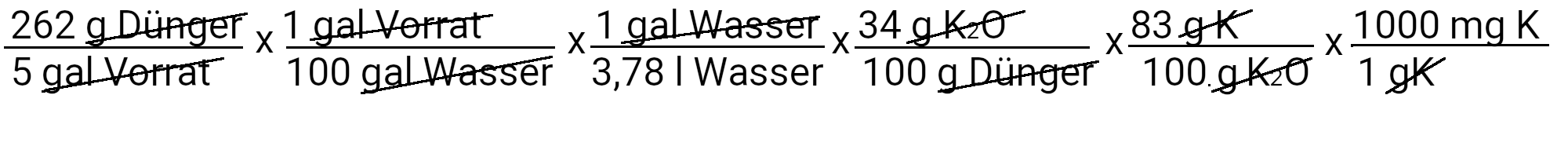
We add 39 mg K / l or 39 ppm potassium. Our recipe provides 210 ppm potassium. If we subtract 39 ppm of potassium from it, we see that we still have to add 171 ppm of potassium.
We have only one other source of potassium, namely potassium nitrate. Let's calculate how much we have to use of it.

We need to add 885 g of potassium nitrate to get 171 ppm of potassium. However, potassium nitrate also contains nitrogen. We use the second equation to determine how much nitrogen should be added in ppm.

We add 61 mg N / l or 61 ppm nitrogen. Our recipe provides 150 ppm nitrogen. We supplied 73.4 ppm nitrogen from calcium nitrate and had to add 76.6 ppm nitrogen. Now we can subtract 61 ppm nitrogen. We still have to add 15.6 ppm nitrogen. The only source of nitrogen that we have is ammonium nitrate.
Let us now calculate how much ammonium nitrate we have to use to deliver 15.6 ppm nitrogen.

We need to add 86.7 g of ammonium nitrate to get 15.6 ppm nitrogen.
At this point we have completed the nitrogen, phosphorus, potassium and calcium part of the recipe. For the other nutrients, we only need to use the first equation, since the fertilizers that we use for their supply contain only one nutrient in the recipe.
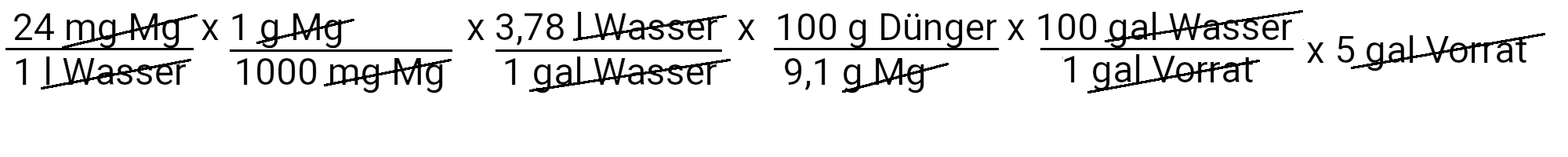
We need to add 498.5 grams of magnesium sulfate to get 24 ppm magnesium.
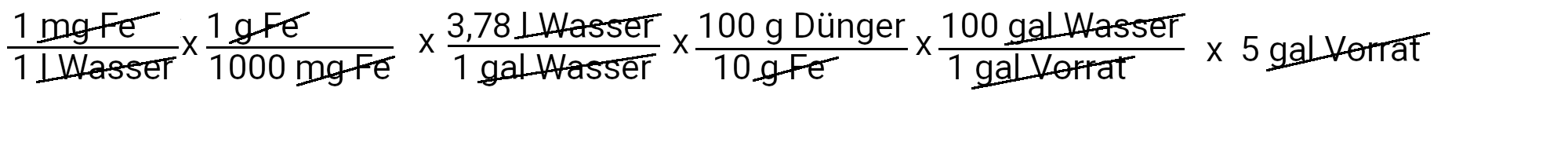 We need to add 18.9 grams of Sequestren 330 to get 1 ppm of iron.
We need to add 18.9 grams of Sequestren 330 to get 1 ppm of iron.
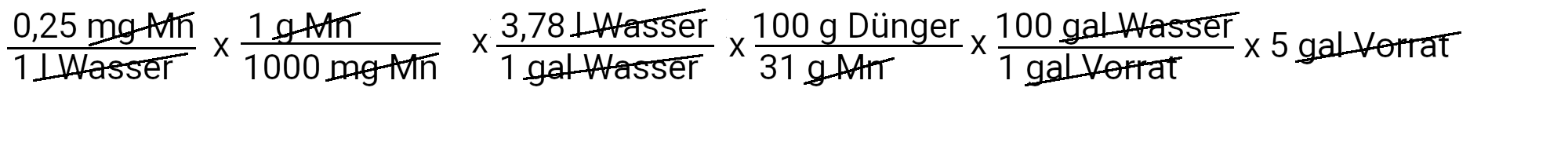
We need to add 1.5 grams of manganese sulfate to get 0.25 ppm manganese.
It is easier to weigh small amounts of fertilizers in milligrams. The conversion from milligrams to grams is therefore carried out as follows

We need to add 692 milligrams of zinc sulfate to get 0.13 ppm zinc.

We need to add 0.17 milligrams of copper sulfate to get 0.023 ppm copper.
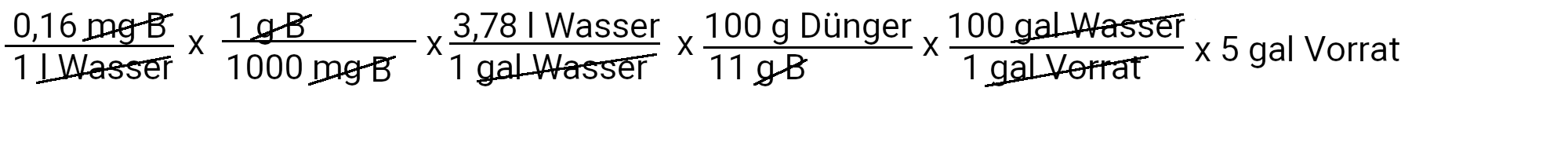
We need to add 2.8 milligrams of borax to get 0.16 ppm borax.

We need to add 0.12 milligrams of sodium molybdate to get 0.024 ppm molybdenum.
Summary:
| Element | Addition | Nutrient Solution |
| Calcium | 895.3 g calcium nitrate | 90 ppm calcium |
| Phosphorus | 262 g of potassium phosphate monobasic | 31 ppm phosphorus |
| Potassium | 885 g potassium nitrate | 171 ppm potassium |
| Nitrogen | 86.7 g ammonium nitrate | 15.6 ppm nitrogen |
| Magnesium | 498.5 grams of magnesium sulfate | 24 ppm magnesium |
| Iron | 18.9 grams of sequestrene 330 | 1 ppm iron |
| Manganese | 1.5 grams of manganese sulfate | 0.25 ppm manganese |
| Zinc | 692 milligrams of zinc sulfate | 0.13 ppm zinc |
| Copper | 0.17 milligrams of copper sulfate | 0.023 ppm copper |
| Boron | 2.8 milligrams of borax | 0.16 ppm boron |
| Molybdenum | 0.12 milligrams of sodium molybdate | 0.024 ppm molybdenum |
Now all calculations have been completed. Now we have to decide in which storage tank, A or B, we give the individual fertilizers. In general, the calcium should be kept in a tank other than the sulfates and phosphates, as they can form precipitates that can clog the drip bodies of the irrigation system. Using this guideline, we can put the calcium nitrate in one tank and the monobasic potassium phosphate, magnesium sulfate, manganese sulfate, zinc sulfate and copper sulfate in the other tank. The rest of the fertilizers can be placed in both tanks.
You should also consider the amount of nutrients in irrigation water. For example, if we use irrigation water that contains 10 ppm magnesium, we only need to add 14 ppm more with our fertilizer (24 ppm Mg, which are required in the recipe, minus 10 ppm Mg in water). This is a great way to use nutrients more efficiently and fine-tune your fertilizer plan.
With some micronutrients, you have to decide for yourself what you want to add. You could do a small experiment to find out whether you need to add 0.12 milligrams of sodium molybdate to your stock solution, for example, or whether you are satisfied with the performance of your plants without this addition.
One last point to consider. Sometimes the calculations don't work as well as here for fertilizers that contain more than one required nutrient, and you may need to add more of a nutrient, than is provided in the recipe to provide the other nutrient.
For example, if you apply calcium nitrate to meet calcium needs, the solution may not contain enough nitrogen. In such cases, you have to decide which nutrient you want to give priority to. For example, you could apply calcium nitrate to meet the plants' nitrogen needs because the excess amount of calcium does not harm the plants. Or you choose to apply it based on the plant's calcium needs because the lack of nitrogen is just a few ppm.
Here you will find what problems there may be with a lack and excess of fertilizer
Context:
ID: 417




